We will be implementing the Neural Network for the Continuous Bag of Words (CBOW) from the word2vec paper. This article assumes you have a good understanding of the high-level of word2vec. This will be covered in coming articles also.

Our goal is to train with sample pairs $(y,X)$, where $y$ is the target word, and $X$ is one of the context words from within the window.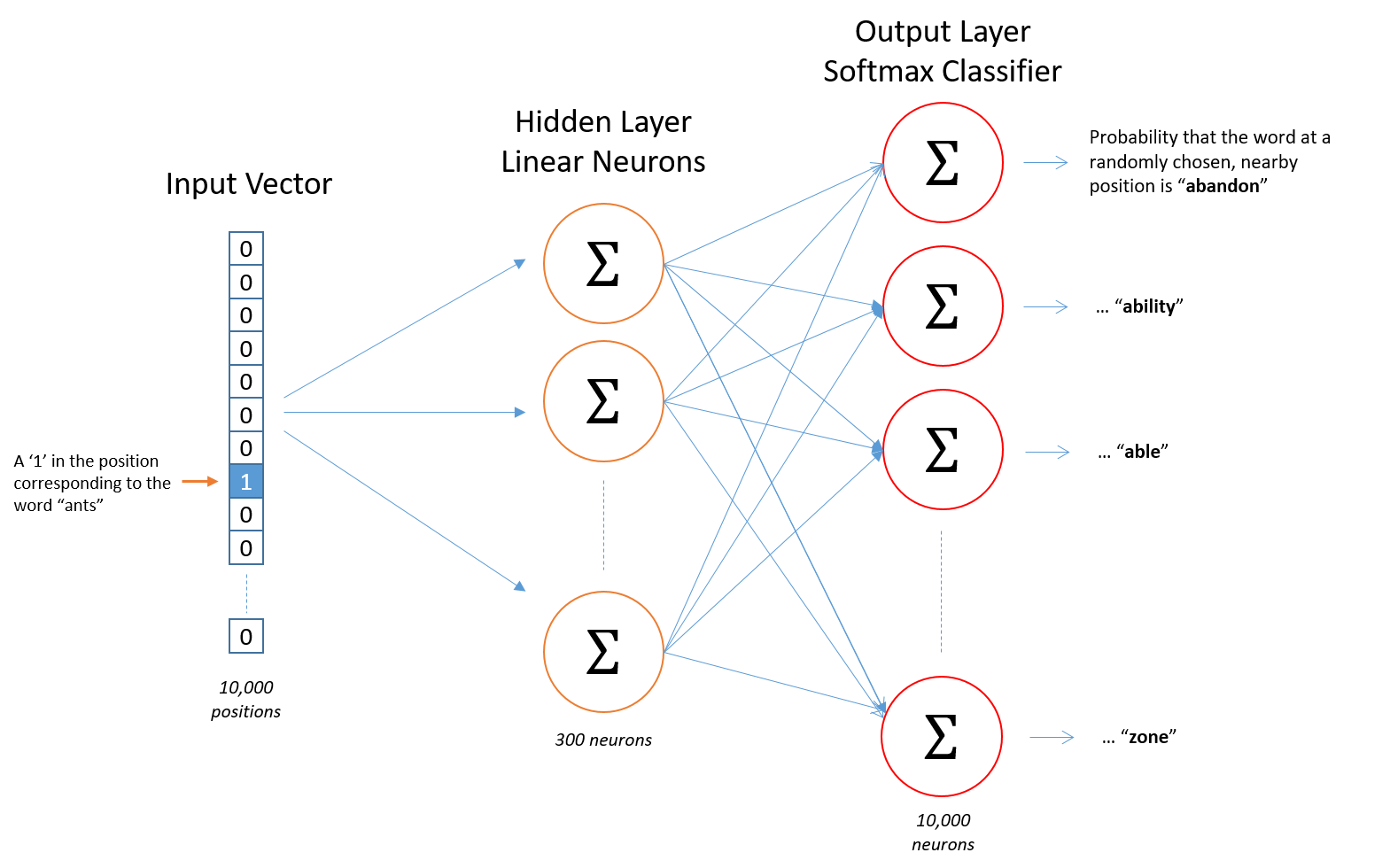

The error function we want to minimise:

• This is negaitve log likelihood, but for our purposes is same as cross entropy loss $$ 1/T \sum\limits_{-c\le j\le c,j\ne 0}^{T} \log P(w_{t+j}|w_{t}) $$

Here is the derivation of cross-entropy loss for backprop: $$ \frac{\partial \mathcal{L}}{\partial A_2} = Z - y $$ so all we need to do is $Z-y$ (where $Z$ is output of NN) when we do backprop

Algebraic form of the NN model: $$ A_1 = XW_1 \newline A_2 = A_1W_2 \newline Z = softmax(A_2) $$

where:

• $X$ is the input vector (for CBOW, a word from the context window)
• $W_{1}$ is weight matrix for the input->hidden layer
• $Z$ is the output of the NN (probabilities of each word)

Pseudocode for the model’s forward() method:

(where @ is dot product)

a1 = X @ w1
a2 = a1 @ w2
z = softmax(a2)

Softmax function:

def softmax(X):
    res = []
    for x in X:
        exp = np.exp(x)
        res.append(exp / exp.sum())
    return res

Pseudocode for backprop:

remember that our loss equation worked out to be $Z - y$

da2 = Z - y
dw2 = a1.T @ da2
da1 = da2 @ w2.T
dw1 = X.T @ da1
assert(dw2.shape==w2.shape)#ensure same shape before update weights
assert(dw1.shape==w1.shape)
#updating weights in model:
w1 -= alpha * dw1
w2 -= alpha * dw2
CEL = crossentropy(Z,y) #for logging purposes (I think)

where: da2 is the derivative of a2 alpha is learning rate cross entropy is:

def cross_entropy(z, y):
    return - np.sum(np.log(z) * y)

default hyper-params:

• iterations: 50
• learning rate: 0.05

Sources:

Code based on work by Jake Tae
Great detailed explanation of Word2Vec by Chris McCormik
Stanford lecture on Word2Vec, which gives more detail on the motivation